Weingarten Surface Approximation by Curvature Diagram Transformation

Abstract

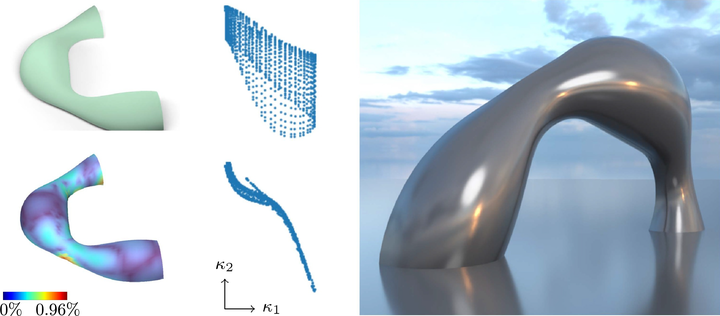
Weingarten surfaces are characterized by a functional relation between their principal curvatures. Such a specialty makes them suitable for building surface paneling in architectural applications, as the curvature relation implies approximate local congruence on the surface thus the molds for paneling can be largely reused. In this work, we aim at a novel task of Weingarten surface approximation. Given a surface mesh with arbitrary topology, we optimize its shape to make it as Weingarten as possible. We devise a curvature-based optimization approach based on the fact that the 2D principal curvature plots of a Weingarten surface comprise a group of 1D curves that encode the curvature relations.Our approach alternatively performs two steps. The first step transforms the principal curvature plots from a 2D region to 1D curves in order to explore the curvature relations.The second step deforms the shape such that its curvatures conform to the corresponding transformed curvature plots.We demonstrate the effectiveness of our work on a variety of shapes with different topologies.Hopefully our work would bring inspiration on the study of general Weingarten surfaces with arbitrary topology and curvature relation.